Schulze Methode
Hier stelle ich euch die Schulze Methode vor.
Allgemein: Die Schulze Methode ist ein Wahlverfahren von Markus Schulze, bei der man die Kandidaten für ein Amt nach seiner Präferenz in eine Reihenfolge bringt. Durch Ermittlung von stärksten Pfaden in einem Graph wird ein Sieger ermittelt.
Voraussetzungen: Zum einen brauchen wir Kandidaten für ein bestimmtes Amt und die Personen, die wahlberechtigt sind.
Jeder Wähler bekommt einen Zettel mit den Namen der Kandidaten. Dort müssen die Wähler Zahlen an die Kandidaten schreiben, welche eine Reihenfolge darstellt.
Je kleiner die Zahl, desto höher platziert ist diese Person. Der Kandidat mit der niedrigsten Zahl wird also als erste Wahl angesehen. Derjenige, der die höchste Zahl hat, ist die allerletzte Wahl. Dabei ist uninteressant, wie groß die Zahl ist bzw. wie groß die Abstände zwischen den Zahlen sind.
Optional ist Folgendes, was aber oft verwendet wird und ich somit im Weiteren als Voraussetzung nehme: Kandidaten, die die gleiche Platzierung haben, werden nicht gegenüber dem anderen bevorzugt. Kandidaten ohne Platzierungen/Zahlen werden gegenüber allen anderen abgelehnt. Es wäre also das gleiche, wenn bei denen der höchste vergebene Platz plus eins stehen würde.

Wie man in diesem Beispiel sieht, ist Sabine die bevorzugte Wahl. Sie wird gegen alle anderen bevorzugt. Sollte sie nicht der Sieger werden, soll es entweder Angela oder Guido werden. Wenn keiner von den dreien es wird, dann ist Karl-Theodor die nächste Wahl. Die letzte Wahl wäre Ursula und Wolfgang.
Es wäre das gleiche, wenn bei Ursula und Wolfgang jeweils die Zahl 4 (oder höher) stehen würde.
Hat jeder der Wähler seine Stimmzettel ausgefüllt und abgegeben, kann es zur Auszählung kommen.
Auszählung:
Nun liegen dem Wahlleiter und seinen Helfern die Stimmzettel vor. Man kann dies per Hand auswerten, was aber einen sehr großen Aufwand bedeuten würde. Deshalb würde ich zu einer Auswertung durch den Computer raten. Dabei müssen aber die Platzierungen von allen Wahlzetteln aufgeschrieben und veröffentlicht werden, um später nachvollziehen zu können, ob das Programm auch richtig gerechnet hat. Dabei würde ich empfehlen, dass von den anwesenden Wählern ein paar Leute darauf achten, dass die Platzierungen richtig notiert werden.
Folgend erkläre ich an einem Beispiel, wie man die Stimmzettel per Hand auswerten würde bzw. was das allgemeine Prinzip ist. Das Computerprogramm macht dasselbe, was aber viel schneller ist.
Auswertung am Beispiel:
Als Beispiel wählen wir folgende Auszählung:
3x a-c-d-b
9x b-a-c-d
8x c-d-a-b
5x d-a-b-c
5x d-b-c-a
Dies zeigt die jeweiligen gewählten Reihenfolgen und wie oft diese abgegeben wurde. ‘a’, ‘b’, ‘c’ und ’d’ sind die Kandidaten. Der Kandidat links wird dem Kandidaten rechts bevorzugt. Ich habe hierbei auf Kandidaten mit gleicher Platzierung verzichtet. Kandidaten ohne Platzierungen werden eh nach ganz hinten gestellt, weshalb es bei dem Beispiel jetzt unerheblich ist, ob eine Zahl dran stand oder nicht.
Ich möchte darauf hinweisen, dass es bei der Schulze Methode verschiedene Wege (Heuristiken) zur Ermittlung gibt und man die Bevorzugung unterschiedlich zählen kann. Im Folgenden werde ich die empfohlene Methode zeigen.
Aus obiger Auszählung ergibt sich folgende Tabelle:
Hier sieht man, dass ‘a’ 16x gegenüber ‘b’, 17x gegenüber ‘c’ und 12x gegenüber ’d’ bevorzugt wird. Dies geht analog bei ‘b’, ‘c’ und ’d’ weiter. Man hat einfach oben geschaut, wie oft der eine Kandidat vor den anderen stand. Hätten zwei Kandidaten die gleiche Platzierung gehabt, wäre dies bei keinem von den beiden Kandidaten eingerechnet wurden, weil Niemand gegenüber den anderen bevorzugt wurde.
Nun sieht man, dass die Tabelle an der Diagonalen symmetrisch (oder wie auch immer man es nennen möchte) ist. So sieht man z.B., dass ‘a’ gegenüber ‘b’ 16x bevorzugt wurde und andersherum nur 14x. Nun sucht man sich die Gewinner der jeweiligen Paare raus:
Ich habe hier die Gewinner markiert.
Nun zeichnet man sich einen Graphen mit den Kandidaten. Die markierten Gewinner aus der Tabelle werden als gerichtete Kanten (Verbindungslinien) mit der Zahl aus der Tabelle als Gewicht eingetragen:
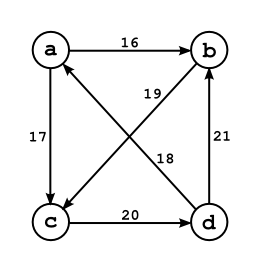
Wie man sieht, werden alle Kandidaten miteinander verbunden. Derjenige, der mehr bevorzugt wurde als der andere, zeigt auf den anderen. Die Anzahl der Bevorzugungen werden an die Verbindung rangeschrieben (die Gegenrichtung wird mit seinen Gewichten/Bevorzugungen weggelassen).
Nun beginnt der spannende Teil, der oft nicht richtig erklärt wird und wo das Verständnis meist aufhört. Aber keine Sorge: Der nächste Schritt ist ganz leicht. ;)
Es werden in dem Graph von jedem Kandidaten zu jedem anderen Kandidaten die stärksten Pfade gesucht. Ein starker Pfad ist hierbei eine Verbindung über andere Kandidaten (Pfad), bei der das niedrigste Gewicht von den Kanten am größten ist.
Schauen wir uns mal den Weg von ‘a’ nach ‘b’ an. Als allererstes kommt die direkte Verbindung infrage. Hier hat die niedrigst gewichtete Kante das Gewicht 16. Der zweite Pfad wäre über die Kandidaten ‘c’ und ’d’ möglich. Dort hat die niedrigst gewichtete Kante das Gewicht 17. Das Gewicht (der niedrigst gewichteten Kante) ist größer als bei der direkten Verbindung und wird somit genommen. Wie man hier sieht, ist die Länge des Pfades egal - es dürfen nur keine Zyklen entstehen. In diesem Beispiel gibt es keine weiteren Möglichkeiten, um von A nach B zu kommen.
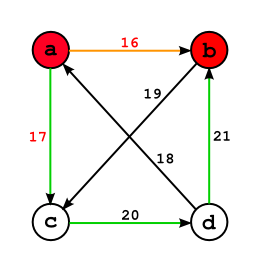
Das geht so analog weiter. Daraus ergeben sich dann folgende Pfade:
Hier wurden die stärksten Pfade mit deren Gewichten dargestellt. Die schwächsten Gewichte der Glieder wurden unterstrichen. Man merkt hier, dass folgendes zählt: “Die Kette ist nur so stark wie das schlechteste Glied”. Nun schreibt man die schwächsten Gewichte (der stärksten Pfade) heraus:
Anschließend schaut man wie am Anfang, wer wen schlägt:
Die Schulze Methode sagt, dass derjenige der Gewinner ist, der nicht von anderen geschlagen wird. Also wenn zwei Kandidaten die gleiche Anzahl haben, ist es nicht schlimm.
In diesem Beispiel hat Kandidat ‘c’ gewonnen, weil dieser alle anderen geschlagen hat. Man kann nun um eine Reihenfolge bestimmen zu können, davon ausgehen, dass nach Anzahl der “Schläge” geht. Somit wäre dies die Gewinnerreihenfolge:
1. c (3x)
2. d (2x)
3. b (1x)
4. a (0x)
Sollte es zu einem Gleichstand kommen (sozusagen mehrere Gewinner, wenn es nur um einen Posten geht), wird z.B. das Ranked Pairs Verfahren empfohlen. Wikipedia erklärt diese Methode ganz gut. Das Problem ist aber, dass dann dort oft ebenfalls ein Gleichstand rauskommt. Daher würde ich empfehlen einen neuen Wahlgang mit einer Stichwahl (zwischen den beiden Gewinnern) zu starten.
Weitere Links / Quellen
Lizenz
 “Schulze Methode” von Christoph Giesel steht unter einer Creative Commons Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Deutschland Lizenz.
“Schulze Methode” von Christoph Giesel steht unter einer Creative Commons Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Deutschland Lizenz.